Fine oar mechanics

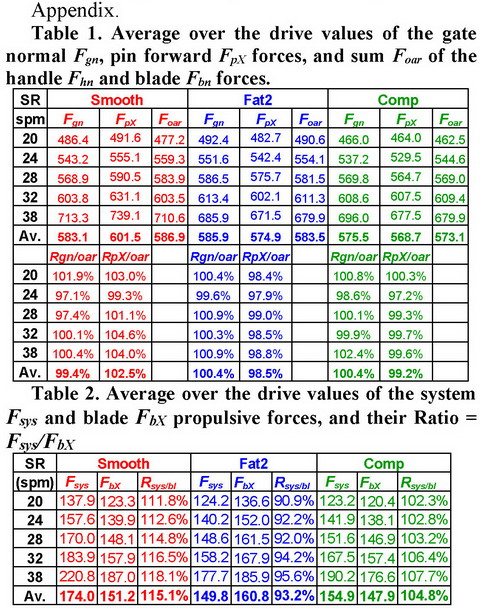
We continue the analysis of oar mechanics with two purposes here: 1) verify checksum of oar forces with the measured gate-pin forces; 2) relate oar forces with the propulsion of the rower-boat system. Four torques and five forces were measured at each oar in the latest experiment. The torques were described in RBN 2020/10-11, the forces were: gate normal force F_gn, gate axial force F_ga, pin X (forward) force F_pX, pin Y (side) force F_pY (Fig.1) and pin Z (vertical) force F_pZ (orthogonal to the plane and not shown on Fig.1). Two oar angles in the horizontal A_oar and vertical planes A_ov were measured at the inboard, which brings the total amount of measured variables to 11 from one oar.

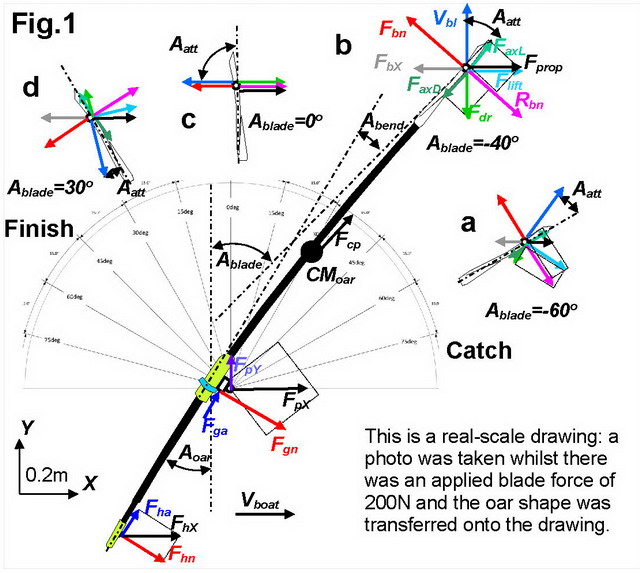
Normal handle F_hn and blade forces F_bn were calculated using the measured torques and derived points of their application (RBN 2020/10). First, it was checked if the sum of oar forces F_oar= F_hn+F_bn is equal to the measured normal gate force F_gn. The pin forward force F_pX was also compared (Fig.2). Average values over the drive (Table 1 in Appendix) were very close with differences within the range ±1.5%, which could be a proof of accuracy: F_gn was slightly higher than F_oar, and F_pX was slightly lower. The curves had slightly different patterns: F_oar was higher than F_gn and lower than F_pX “before the pin” (1), but “after the pin” the differences were reversed (2), so their curves are nearly mirrored (Fig.2,b).

This finding was quite surprising because the forward pin force F_pX depends on the oar angle. So, the average value of F_pX should be lower than F_gn, unless the axial gate force F_ga contributes enough to balance the oar angle effect, and it looks like it does.

The second issue is to verify the propulsive force derived within the rower-boat system (RBN 2019/01-02) with the propulsive force generated by the blade. The bend of the oar shaft caused by the outboard torque M_out creates an extra blade angle A_bend, which was obtained experimentally and found nearly the same for all oars (even with the extra-soft Fat2 oars):

A_bend = 0.02652 M_out                                  (1)

This means, at the peak force, the blade angle differs by nearly 10 deg from the oar angle measured on the inboard (Fig.1). The blade propulsive force F_bX was calculated as

F_bX = F_bn cos(A_oar + A_bend)                        (2)

The system propulsive force was calculated as the difference between the pin and handle X forces:

F_sys = F_pX - F_hX = F_pX – (F_hn cos(A_oar) + F_ha sin(A_oar))    (3)

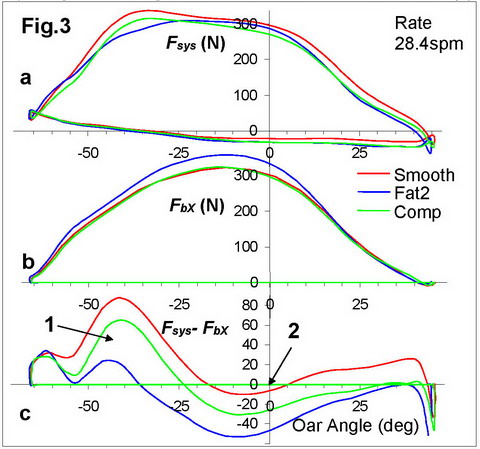
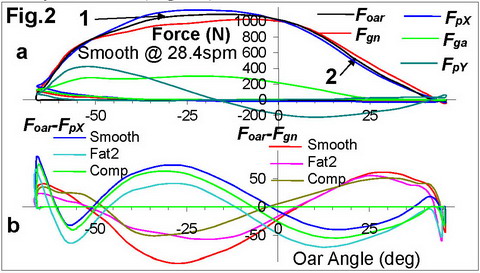
It was found that F_sys was higher after the catch till about -25 deg oar angle (Fig.3), then F_bX dominated “around the pin”, and finally F_sys was higher again until the finish. The differences between F_sys and F_bX significantly vary between the blade types (Fig.3,c) as well as the ratios of their average values over the drive: in Smooth, average F_sys was 15.1% higher than F_bX, in Comps – 4.8% higher, and in Fat2 – 6.8% lower (Table 2 in Appendix). The first suspicion after these surprising findings was that there was a calibration error, but this is improbable because the same gate and pin force sensors were used for all oars with only about half an hour interval. Torque sensors on the oars were also calibrated with the same force sensor and carefully verified.

The hypothesis explaining this paradox is as follows: When the blade moves through the water at a certain velocity V_bl and angle of attack A_att (between the blade axis and vector of its velocity in the water, Fig.1), this creates two forces: parallel with velocity and oppositely directed drag F_dr and perpendicular lift F_lift forces. Their vector sum in the orthogonal direction to the blade is the normal blade reaction force R_bn, which has the same magnitude and opposite direction to the normal blade action force F_bn used to derive the blade propulsive force. However, these drag F_dr and lift F_lift forces are also projected onto the blade axis and create axial forces, which act in opposite directions to each other. Magnitudes of these axial forces depend on the angle of attack A_att as well as on the blade lift C_l and drag C_d coefficients, and the last two depend on the blade properties (the shape, smoothness of the blade surface, etc.). The resultant of the axial force components is transferred along the oar shaft and affects the measured pin and gate forces, as well as the total propulsive force acting on the rower-boat system.

After the catch, at sharp angles of attack (Fig.1,a-b), the lift force is the most significant, its axial component is directed forward and overcomes the axial drag component directed backwards. This could be the reason why the system propulsive forces were measured higher than the blade propulsive force at the oar angles from -50 to -25 deg “before the pin” (Fig.3,1).

At oar angles close to 0 deg during the middle of the drive (Fig.1,c), the vector of blade velocity is nearly perpendicular to its axis (the angle of attack is about 90deg), the lift force is absent and only drag force acts on the blade, which has no axial component here. Smoothie blades had nearly zero balance of the system F_sys and blade F_bX propulsive forces (Fig.3,2), which is logical, but other blades had a negative difference F_sys-F_bX: Fat2 blade had significantly higher blade force (because its bigger area and shorter actual outboard - lighter gearing), but without gain in the system propulsion, and Comps had lower system propulsion (?) at a similar blade force with Smoothies. We can only guess that the reason is the rotation of the blade in the water, which creates some resistance, consumes energy and decreases the system propulsion in this way.

“After the pin” to the finish, the angle of attack is getting sharper, so the axial forces affect the system propulsion again: the lift axial component pushes the oar forward, drag axial force pulls it backwards. The Smoothie blade looks the most efficient here and has a positive F_sys-F_bX balance, which could be related to lower drag force without Vortex strips.

Another factor in the balance of the forces is the centripetal force F_cp, which is created at the oar rotation because its CM is located outside of the centre of rotation on the outboard, and this force is always axial. “Before the pin”, this force is directed forward and increases the system propulsive force, “after the pin”, it works backwards and decreases propulsion. Though this force should be quite low, it still may affect the balance of the system and blade propulsive forces: it was higher “before the pin” and lower after it, which looks quite logical.

Concluding: Fat2 has a higher propulsive blade force due to bigger blade area and shorter actual outboard, but this was not converted into an advantage in the rower-boat system propulsion. Contrarily, lower propulsive blade forces in Smoothies and Comps could be compensated by a higher blade velocity through the water due to a longer actual outboard, which creates an additional lift transferred as an axial oar force into the system propulsion. In addition, Smoothies and Comps may have lower drag force compared to Fat2 due to a smaller area, which also contributes to their higher system propulsion.

Complete analysis of propulsive forces acting on the oar-boat-rower system is not a trivial task, and its fine balance still not possible to obtain even with 11 variables measured from one oar. Measurement of the axial force on the outboard may help to complete the puzzle, but this could be quite challenging technically. Experiments with simultaneous testing of the blade types may help to conclude on their efficiency based on speed/power ratio, and we plan to conclude these in the near future.

Acknowledgements: Thanks to Concept2 Inc. and personally to Dick Dreissigacker and Alex Dunne for the interest and kind support of this study.

©2020 Dr. Valery Kleshnev www.biorow.com