Total Rowing Gearing

Gearing ratio is a popular, but contentioustopic in the rowing community. So, what is themechanically correct definition of rowing gearing? For any transmissionmechanism, the gearing Rgis the ratio of displacements/velocities at output to input (Lout to Lin),and it is inversely proportional to the ratioof the corresponding forces (Fin to Fout),which is proven by ArchimedesŌĆÖ law of thelever:
Rg = Lout / Lin = Fin / Fout (1)
So the more you gain in velocity,the more you lose in force and vice versa, but a gain in power is not possible dueto the conservation of energy. It is important to remember, that the standard gearing definition is based onthe ratio of displacements or velocities, not forces, because forces dependon other factors such as friction and inertia of parts in the mechanism.Also, forces are more difficult to measure.
In cycling, gearing is defined as biketravel per crank revolution, and depends on the ratio of the teeth number of the front chainring and the sprocket on therear wheel, and on the size of the rear wheel: e.g. with52/13 teeth chainring/sprocket and a 26ŌĆØ wheel, a bike would travel 8.29m per crank revolution, or 36.2km/h at 80rpm. To be biomechanically correct, the length of the cranks should also be taken into account: with longer cranks, pedal travel would be longer per revolutionand vice versa. With 175mm cranks, pedalstravel 1.10m per revolution, so the total gearing of the bike above would be7.55:1, which mean a bike would travel 7.55m per each meter of pedals travel.
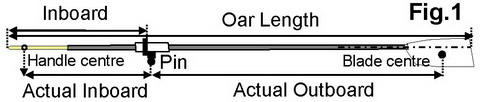
How do we usually define gearing ratio in rowing? Most rowers use the overall oar length (measured from the tip of the handle to the outer edge, Fig.1) and the inboard (from the tipof the handle to the outer face of the button (collar), then calculate the outboard subtracting the inboard fromoar length and gearing = outboard/inboard. However, the oar gearing defined inthis way would not be correct for the following reasons:
1. Thehandle force is not applied at the tip of the handle, but approximately at its middle, so the actual inboard should be counted from thispoint, assumed to be 6cm away from thetip in sculling and 15cm in sweep.
2. Theoar doesnŌĆÖt rotate around the button edge, but around the pin, which is locatedat some distance from the button (usually about 2cm), which should be added tothe actual inboard and subtracted from the actual outboard.
3. Thecentre of water pressure at the blade is not located at its outer edge, but assumedto be close to its centre, so theeffective outboard measurement must be counted tothis point. Therefore, the static oar gearing is defined as the ratio ofactual outboard Lout.a to actual inboard Lin.a:
Oar gearing = Lout.a / Lin.a (2)
At a typical sculling inboard of 88cm, an oarlength of 288cm and blade length of 45cm, the actual oar gearing is 2.089. Whenaccounting for the measurement discrepancies outlined above it would be 2.273,which is 8.8% higher.
A shorter inboard and longer oarlength/outboard make the gearing heavier, and vice versa: at 87/289 and thesame blade length, the actual oar gearing is 2.139 (2.4% higher/heavier thanabove); at 89/286, it is 2.029 (2.9% lower/lighter). As the effective gearingdepends on blade length, it must be taken into account: e.g., with the shorterConcept2 ŌĆ£CompŌĆØ blade of 37cm, the actual gearing at 88/288cm above would be2.137, or 2.3% higher-heavier than with the standard blade length of 45cm.
The static oar gearing defines onlya part of the very complicated chain of power transmission in rowing. To definethe totalgearing of a rowing vehicle (rower-boat system) in a similar way to cars and bikes (as the ratio of the vehicle speed to thespeed of the engine-rower movement), the following factors should be accountedfor:
1. The oar is disconnected from the transmission throughthe water during the recovery phase. If a cyclist stops pedalling when goingdownhill or by inertia, then their bike wouldtravel longer distance per revolution than is defined by their bike's gearing. This factor can vary randomly, so in real world conditions, the number of crank revolutions per mile is always different. Inrowing, the distance travelled by inertia during the recovery is also random,it depends on the specifics of each crew (their rhythm, stroke rate, forceapplied, etc.) and weather conditions (head or tail wind). Therefore, thedistance per stroke cycle, or ratio of the stroke rate to rowing speed wouldnot define the rowing gearing correctly. The distance travelled during thedrive phase would work for this purpose, but thisrequires special biomechanical measurements.
2. The oar blade works in the water, which is a liquidand canŌĆÖt providea firm connection between the boat and theenvironment, contrarily to cars and bikes (though their wheels may also skid onslippery surfaces). Therefore, a slippage ofthe blade must be subtracted from the output (blade) speed, which makes the rowingvehicle slower relative to the water and gearing lower-lighter. A larger bladearea usually has less slippage and makes the gearing higher (heavier), and viceversa. The slippage reduces the blade efficiency, because part of the energy isspent on movement of the water instead of moving the boat: as if one rides abike with the wheels constantly skidding. The blade efficiency ranges within 70-90%depending on the boat and blade types, weather conditions and the blade paththrough the water, which makes the gearing lighter by 10-30%.
3. Contrary to tyres on a car or bike, which push the ground directly backwards,the blade movement through the water iscurvilinear, it is directed backwards only at the perpendicular oar positionrelative to the boat. At all other points during the drive, a blade moves atvarious angles relative to the direction of boat travel, which creates ŌĆ£a wedge effectŌĆØ (RBN 2014/06): the propulsive component of the force decreases, but thevelocity of the blade relative to the water increases, resulting in heaviergearing. As the oar angles always vary during the drive, the gearing alsochanges, so it is called ŌĆ£dynamic gearingŌĆØ(RBN 2007/03). Similar effects can be found inmany other locomotions: skating/skiing, swimming, birds flying, sailing, etc.(RBN 2019/12).The further the oar is from being perpendicular to theboat the heavier the gearing becomes: at a 60┬░ angle,the static oar gearing must be multiplied by two, at 70┬░ ŌĆō by three. This means, dynamic gearing has a similar or even higher effect than the static oargearing: every 1┬░ increase of thecatch angle increases the gearing ratio as muchas a 1 cm longer outboard, or 0.5cm shorter inboard.
Rowing half-slide would worksimilar to a 15cm shorter outboard and 12% lighter gearing, which rowersusually use at the start of the race for faster acceleration of the boat, and during the final sprintwhen they are fatigued. To know your real gearing, it is important tocontrol the oar angles, which can be done simply with our BioRow AngleGuides, or with NK EmPower instrumented oarlocks.
Many rowers and coaches still define gearing asspan/spread, which is completely incorrect from a mechanical point: moving thefulcrum around simply moves the entire oar further away or closer to the boat,its gearing ratio wouldnŌĆÖt change. However, the span/spread has a strongindirect effect on the gearing, which rowers really feel and this idea is solong lived.
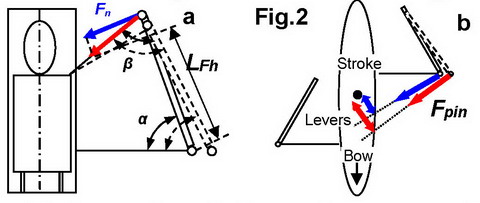
Firstly, span/spread changes the geometry ofthe oarŌĆōrowerŌĆÖs arm connection (Fig.2,a): narrowerspan increases the oar angle ╬▒, so it makes the dynamic gearing heavier; andvice versa. Also, it changesthe angle ╬▓ between therowerŌĆÖs arm and the oar: moving the pin inwards makes it sharper, which reducesthe normal component of the handle force Fn and its torque, so a narrower span works as a shorter inboard, and heavier gearing; awider span works as a lighter gearing in this indirect way. These effects ofthe span work only at catch angles, and they have no effect at the middle ofthe drive.
Secondly, in sweep rowing, especially in apair, the span works as a lever of the rotational moment of the boat relativeto its centre (Fig.2,b). A wider span offsets the line of pin force away fromthe boat centre, which makes its leverage longer and torque higher for the sameapplied force. So, a rower with a widerspan would have an advantage in turning the boat, which could be felt as alighter gearing.
In attempt to define the total rowing gearing,there is another difference from other vehicles, where an engine is firmlyfixed relative to a transmission. In rowing, rowerŌĆÖs mass move significantlyrelative to the boat, so its travel and average velocity during the drive isdifferent from the boat velocity. So, what velocity should we use for therowing ŌĆśvehicleŌĆÖ? The boat, or the rower/crew? The systems centre of mass (CM)?The last is quite close to the crewŌĆÖs CM, as the crew is the heaviest part ofthe system. Having biomechanical data of the handle, boat, and rowerŌĆÖs CMdisplacements and velocities we can derive instantaneous gearing (Fig.3) andits average values during the drive (Table 1):
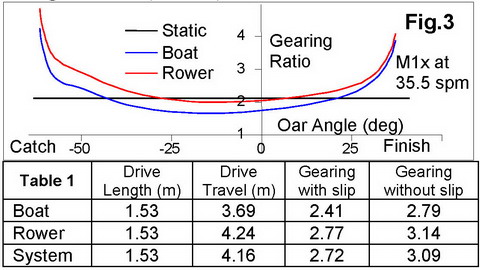
As the rower moves faster than the boat duringthe drive and travels a longer distance, their gearing is heavier than the boat.At the catch and finish, the total gearing is significantly heavier than thestatic one (black line, 2.089 in this case at 88/288) because of the dynamicoar gearing effect. In the middle of the drive, the total gearing is lighter,because of slippage of the blade in the water, of which in this case the totaldistance was 0.57m. So, without the slip, the gearing would be heavier by15.5% for the boat and 13.5% for the rower. The travel of the rowing ŌĆśvehicleŌĆÖover the stroke cycle was 8.38m (it is the same for the boat and rower), so ifwe relate it to the handle travel, overall gearing per cycle would be 5.48.
Compared to cycling, rowing gearing during thedrive is similar to riding a bike on quite a low gear, say, 34/23 on 26ŌĆØ tyres, but pedalling onlyabout half of a revolution and going idle during the remaining half. Comparisonof total gearing over the cycle would be similar to medium bike gear, say,53/19.
Recently, we have developed HDF indicator(Handle Drag Factor, RBN 2020/04-5) and its modification ME (Mass-Equivalent),which indicates heaviness, ŌĆ£a burden factorŌĆØ of rowing and could be used forevaluation of rowing gearing in various conditions, boat types, and riggingsettings.
┬®2020 Dr. Valery Kleshnev www.biorow.com
Is this article interesting and helpful in you rowing or coaching?
If you like this article, please help us to continue research and information services in rowing.
Please support our current research project, which you can find here: http://biorow.com/products/biorow%20books/research_2020
Donations will be asknowledged in our future publications.



