Review on blade propulsive efficiency

Blade efficiency is very popular topic in rowing community discussions, and opinions are still quite controversial. The most “old-fashioned” idea is that long oar angles at the catch make the blade work inefficient, because “the oar pushes the pin inwards instead of moving boat forward”. This myth is quite easy to disprove with understanding of a very simple fact: power is the scalar product of the force and velocity vectors (magnitudes multiplied by the cosine of the angle between them), so when these two vectors are perpendicular one to another (cosine 90^o = 0), the power production equates zero. As the sideways force at the blade/pin is perpendicular to the boat velocity, it does not produce any waste power by itself (RBN 2006/06). Longer catch angles only make the oar dynamic gearing heavier (similar to riding a bike on high gears), but it do not create energy losses by itself nor does it decrease the blade efficiency.

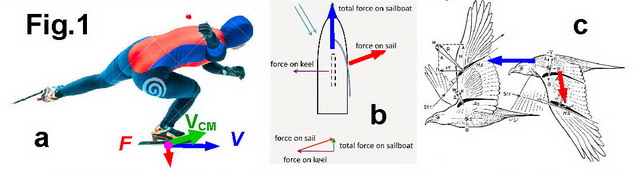
A similar effect of dynamic gearing can be found in other cases, which helps to achieve a higher locomotion speed at lower speed of the propulsive force (Fig.1):

·        In speed-skating or cross-country skiing, the athlete applies force at the skate/ski sideways, but can go faster forward than runners, who apply propulsive force directly backwards;

·        In sailing, boats can go faster at side and even at cross-head wind than at direct tail wind;

·        Birds swing their wings up and down (quite slowly sometimes), but fly forward.

·        Swimmers and canoeists move the hand/paddle sideward to increase propulsive efficiency.

The correct definition of the blade efficiency is also similar to other locomotions: this is a part of the total power production spent on the propulsion of the athlete-equipment system (Fig.2). When a runner pushes from soft soil (sand or snow) or a slippery surface (ice), the point of support at the ground moves, and part of the power is wasted on it, which decreases propulsive power and efficiency, which makes this sort of running slower. The water is always “soft”, so when rowers apply a force at the blade, it slips through the water, which creates movement of the point of support and some wasted power P_w, which can be defined as a product of the blade force F by velocity of its slippage through the water Vbl and by cosine of the angle φ between their vectors:

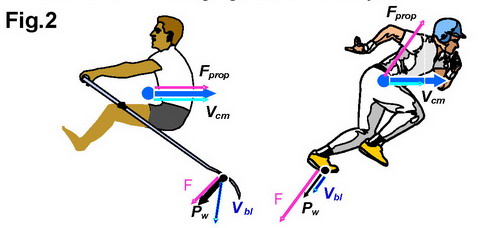
Pw = F Vsl cos(φ)                                           (1)

This wasted power Pw is subtracted from the total rowing power P, and the remaining part is propulsive power P_prop, which moves the rower-boat system forward. The general definition of the blade propulsive efficiency E_bl is the ratio of the propulsive power to the total power P:

E_bl = P_prop / P = (P – P_w) / P                            (2)

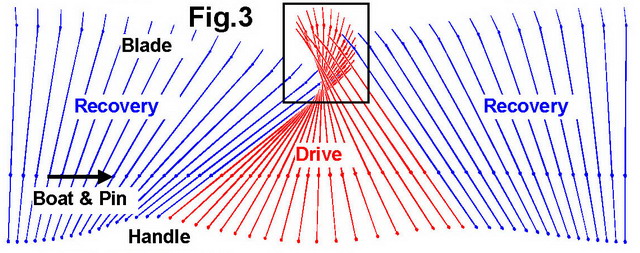
With BioRow telemetry system, we can measure very accurately oar angles and boat movement, use this data to reconstruct the oar path during stroke cycle (Fig.3) and get a picture similar to video from the top.

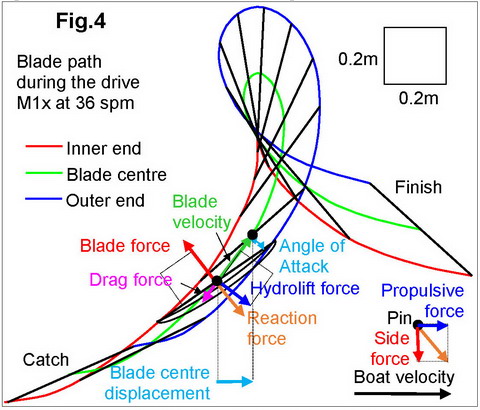
With more detailed analysis of the blade movement during the drive (Fig.4), we can derive the velocity vector Vbl at its centre, an angle of attack Aa of the blade relative to the water (it is important to take into account the bend of the blade), and a force applied to the centre of the blade Fbl could be derived from the measured handle force and gearing ratio. In this case, the centre of the blade moves forward with the boat from the catch to the oar angle about -25 deg before the pin, and then again from about 15deg after the pin till the finish, so it moves backwards only about 35% of the drive time and slips backwards only about 12cm. The outer tip of the blade slips more (about 30cm), but the inner edge doesn’t slip backwards at all and always moves forward with the boat. During the total drive time, the blade centre moves 1.68m forward with the boat.

If the blade moves through the water at the angle of attack Aa different from 90^o, it creates a hydro-lift force Flift, so the blade works as a foil (RBN 2007/12). The lift force Flift always has orthogonal direction to the blade velocity vector Vbl, therefore, this force never consumes any power and has 100% efficiency. All energy losses depend on the drag force Fdrag, which acts in the opposite direction to Vbl. Flift and Fdrag are components of a total blade reaction force Freact, which has the same magnitude and opposite direction as the blade action force Fbl. Freact is transferred through the oar shaft to the pin and can be decomposed to the propulsive force Fprop, which moves the whole system forward, and side force Fside, which does not create any energy losses, because it is perpendicular to the boat velocity. It is important to understand that, any slippage of the blade in the water creates energy losses, no matter which direction, even if the blade moves forward with the boat as it mainly does during the drive.

Averaged through the drive, the hydro-lift force Flift provides about 56% of the total blade force (Fig.5) and Fdrag contributes to the remaining 44%. Total distance of the slippage of the blade centre along the whole curvilinear blade path was 1.7m, overall blade efficiency was 78.5%.

An equation defining the blade efficiency is quite complex (RBN 2012/06) and includes the blade velocity Vbl , force Fbl , and angle of attack Aa, as well as water density ρ, the area of the blade S, and the combined drag factor of the blade k (which depends on the blade shape and the angle of attack):

Ebl = 1 – sin(Aɑ) /(k ρ S)^0.5 Fbl^0.5/ Vbl       (3)

This equation can be useful for defining the following factors affecting the blade propulsive efficiency.

1.      The blade efficiency is higher, when the angle of attack is sharper (sin Aɑ is lower), which happens at the beginning and the end of the drive.

2.      The blade efficiency is higher, when any of the multipliers k, ρ or S increase: the blade shape is more efficient (k↑), and/or the water is denser (ρ↑), and/or the blade area is bigger (A↑).

3.      The blade efficiency is higher, when the blade force Fbl is lower, which, again, happens at the beginning and the end of the drive, and (in combination with sharper angles of attack) explains the rise of the efficiency curve. At the same handle force, the blade force is lower at shorter inboard and/or longer outboard, so the blade efficiency is higher at a heavier gearing ratio. If the blade force Fbl is getting close to zero, its efficiency approaches 100%, but the blade doesn’t work for propulsion and becomes useless. For this reason, the stronger rowers in a crew usually have lower blade efficiency, and vice versa (with some exceptions, however RBN 2018/08).

4.      The blade efficiency increases, if the blade velocity Vbl became higher, which happens at a faster boat velocity. This explains why the blade efficiency appeared to be higher in faster / bigger boats and at faster weather conditions (tail wind), though the real slippage of the blade could be the same - the blade doesn’t work better in the water.

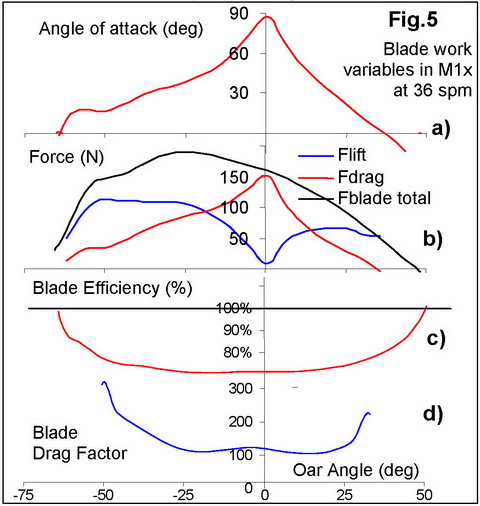
The last point above indicates that the blade efficiency may not be a completely adequate measure of the quality of the blade work, so we tried to find another indicators for it and developed the blade Drag Factor DF_bl concept (RBN 2018/05-07, Fig.5,d), which is the ratio of the blade force F_bl to the square of its slip velocity V_bl in the perpendicular direction (DF_bl = F_bl / V_bl²). Blade DF_bl does not depend on the boat velocity, but it gets very high at the beginning and end of the drive, when the blade slip velocity is low, making it more difficult to analyse. It was found that average DF_bl (400+) is more than 100 times higher than the boat DF (~3 in 1x), and this is a condition, which makes it possible to move the rowers-boat system forward.

With its average 80% efficiency, the blade is a quite effective propulsive device. From the total rower energy losses, less than 6% is spent on the slippage of the blade, and the main part is lost in the rower’s body. Some factors have an opposite effect on the blade and rower’s efficiencies, and attempts to increase the former may decrease the latter and therefore decrease overall rowing efficiency: for example, heavier gearing and bigger blade area increases blade efficiency as it was shown above, but it makes the handle velocity much slower, which could be inefficient for a rower (RBN 2007/09), as it makes the drive time longer, decreases the stroke rate and rowing power, and so the rowing speed. Also, a bigger blade is more difficult to handle at the catch and finish, and it may create a higher aerodynamic drag during recovery.

Other factors have a similar effect on various efficiency components: as the blade efficiency is higher at the beginning and end of the drive, it is beneficial to increase force quicker after the catch and maintain it higher before the finish, in other words, to make the force curve more rectangular. This is also good to the total power production and effective dynamics of the rowing system.

Concluding: the blade propulsive efficiency and drag factor could be used for evaluation of the equipment quality and rower’s oar handling skills, but for the best rowing performance, other components of the system must be taken into account to find an optimal balance.

©2019 Dr. Valery Kleshnev www.biorow.com