Balance of Propulsive Forces

 Balance of Propulsive Forces

In this newsletter I continue analysis of forces in rowing, and focus here on the balance of propulsive forces. The force Fb_x acting on the boat was previously defined (RBN 2019/01) as the difference between the pin Fp_x and stretcher forces Fs_x:
Fb_x = Fp_x – Fs_x                                         (1)

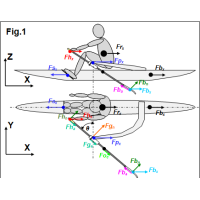
The propulsive force applied to the rower’s centre of mass CM Fr_x was defined as the sum of reaction forces at the stretcher Fs_x and the handle Fh_x (Fig.1), where the latter Fh_x is the sum of X components of normal Fh_n and axial Fh_a forces at the handle. The latter Fh_a was assumed to be equal to the measured axial gate force Fg_a, but in fact they could be slightly different because of the axial blade force Fb_a and centripetal force of oar rotation Fo_c acting only on the gate axial force Fg_a.
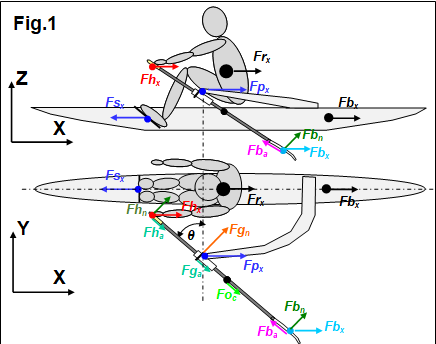
Fr_x = Fs_x - Fh_x = Fs_x – (Fh_n cos(θ) + Fg_a sin(θ))    (2)
where θ is the oar angle. Fig.2 shows these forces in M1x at 35.5spm, the same sample as in RBN 2019/01.

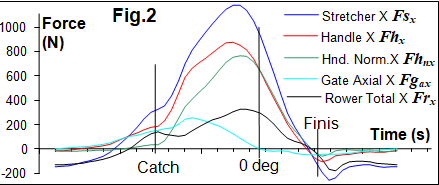
The propulsive force applied to the rower-boat system Fpsys_x was defined as the sum of the forces on the boat Fb_x and rower’s CM Fr_x (Eq.1,2). The stretcher force Fs_x is cancelled, so Fpsys_x is the difference between X forces at the pin Fp_x and handle Fh_x:
Fpsys_x = Fr_x + Fb_x = (Fp_x – Fs_x)+ (Fs_x - Fh_x) = Fp_x - Fh_x (3)
Therefore, the stretcher force is not accounted in the system propulsive force at all, being an internal force between the boat and the rower’s mass. The propulsive force acting on the rower-boat system is the difference between X components of the pin and handle forces. However, this doesn’t mean a rower should minimise the stretcher force, as it is firmly transferred through the boat-rigger to the gate-pin force, which reaction counterpart is the main positive component of the system propulsive force.

During the middle of the recovery, Fpsys_x is close to zero as expected (Fig.3,1), but the system propulsive force becomes positive even before the catch (2), which could be an effect of the oar centripetal Fo_c and rotational inertia force F_o.in (RBN 2015/05). During the recovery, the oar CM (located on the outboard) moves forward, so it’s kinetic energy is transferred to the system at oar deceleration before the catch (2). After the finish, the oar inertia force is negative, which decreases the system propulsive force (3).

The X component of the oar inertial force was defined with the angular oar acceleration α derived from the oar angle, the oar moment of inertia Io at the pin (1.6 kgm²) and distance between CM and the rotation axis Lo_CM (0.42m from pin):
F_o.in = Io α / Lo_CM cos(θ)                          (5)
Oar inertia force explains the increasing of the total propulsive force before the catch (Fig.3,2) and its drop after the finish (3).
The total propulsive force measured from the pin/gate and handle Fpsys_x was compared with one used traditionally as the forward component of the blade force Fb_x defined through the handle force Fh, gearing ratio (inboard L_in to outboard L_out) and oar angle θ:
Fb_x = Fh (L_in/L_out) cos(θ)                         (6)

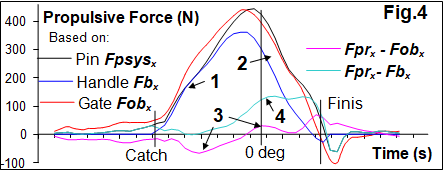
These two forces were quite similar during the first half of the drive (Fig.4,1), but then, Fpsys_x appeared to be much higher than Fb_x (2). To eliminate sensor error, the propulsive force at the blade Fob_x was derived from the oar sensors, which were completely independent from the pin sensor:
Fob_x = (Fg_n – Fh_n) cos(θ)                         (6)
where Fg_n is the normal gate force and Fh_n is normal handle force. Two forces Fpsys_x and Fob_x matched quite well together - a small difference between them (3) could be related to the axial force at the blade Fba_x and oar centripetal force Fo_c, which were not measured from the oar sensors in Fob_x, but affected the total propulsive force Fpsys_x.
The significant difference in Fpsys_x-Fb_x during the second half of the drive (4) could be explained by a shift of the centre of pressure at the blade inwards, which decreases actual outboard and increases the blade force, so Fb_x defined through the handle force and gearing appeared to be underestimated. This was my previous idea, when I analysed changing the ratio of handle/gate forces (RBN 2014/02).
To verify that the above increase of the blade force is true, various versions of the propulsive force were averaged over the stroke cycle at various stroke rates (17.2-41.5 spm) and speeds (2:16-1:31 s/500m). The drag force at the boat hull (RBN 2019/01) was also averaged, all these four forces were used to plot relative speed, then power trend lines were built over the data points (Fig.5).

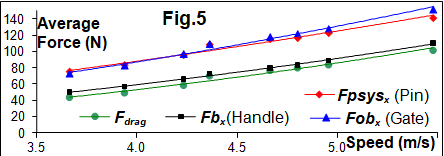
The best match was found between the drag force and Fb_x - the blade propulsive force obtained with the traditional method of using the handle force only (r=0.991). On average, the blade propulsive force was 8.3% higher than the boat drag force, which can be easily explained by additional air drag resistance. Two other versions of the propulsive force also had very high correlation with the drag force (r=0.998), but Fpsys_x (obtained from pin-handle) was 53.2% higher, and Fob_x (from gate-handle) was 57.1% higher than the drag force. This placed doubts on my previous hypothesis about there being shorter actual outboard and higher blade force during the second half of the drive.
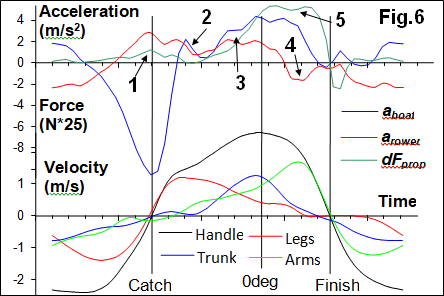
A possible solution to this puzzle, the mysterious extra force at the pin-gate, is to relate it to some inertial force in the rower-boat system. To do this, the found above difference in propulsive forces dF_prop = Fpsys_x- Fb_x was compared with accelerations of the boat a_boat and rower’s CM a_rower (Fig.6), where a_boat was measured directly and a_rower was derived from measured seat and rower’s trunk movements added to the boat acceleration. Velocities of the handle and rower’s body segments are given as a reference of the phases of the stroke cycle.
Here, I should refer to my model of power conversion into kinetic energy (RBN 2018/11), where point 9 can be appended as follows: “Two components of the system, the rower and the boat, not only receive kinetic energy through the oar, but also exchange it between themselves. … Energy exchange also happens during the drive: after the catch, the rower actively accelerates his CM using the leg drive, taking kinetic energy from the boat, which receives negative acceleration”. At the catch, this exchange happens through the stretcher force, which is not accounted in propulsion equation No. 3, so it is not reflected in the difference of propulsive forces dF_prop. A small value of this difference at the catch (Fig.6,1) could be related to oar linear inertia force, which pushes the pin and looks like propulsive force.

During the beginning of the drive, the boat acceleration became similar to the rower’s CM acceleration (2), so no exchange of kinetic energy happens between them, and dF_prop gets close to zero.
In the middle of the drive, the boat acceleration became higher than the rower’s acceleration (3), then the latter became negative (4). This means that the rower transfers kinetic energy to the boat, which happens through the gate-pin forces, but is not related to the blade propulsion and reflected in the highest difference of forces dF_prop (5).
To understand these mechanics better, the following example can be used (suggested by Dr. Volker Nolte, although for another reason). Imagine that a rower moves back and forth in the boat with the oar firmly fixed in the oarlock without rotation, with no blade work in the water, and only the gate force is measured. At the “catch”, the rower pushes the stretcher, but this force is not counted as it is an internal force. At the end of the “drive”, the rower needs to decelerate his movement and pull the handle, which is measured as the gate force and looks like “propulsive” force.
Currently, all this is a hypothesis and there is still a lot of work required to understand the mechanics better and to develop methods of analysis for propulsive and internal forces in the rower-boat-oar system. Say, in the example above, the rower pulls the fixed oar producing the handle force, which subtracted from the gate force in eq.3, so “propulsive” force should be zero. Perhaps, some other factors are at play here: Gearing? Seat friction? Axial oar forces?
In conclusion, the  mechanics in the rower-boat-oar system are quite a complex issue, where the main challenge is separation of propulsive and internal forces mixed in the measurements at the handle, gate-pin and stretcher. Currently, a complete explanation for the phenomenon of higher gate-pin force during the second half of the drive is still not completely clear to us. All suggestions and hypotheses are very welcome.
Acknowledgements: Thank you to WinTech Racing Boats and Oarsport Ltd. for their support of this study.
©2019 Dr. Valery Kleshnev www.biorow.com