Discussion on Power in Rowing
Recently, there have been discussions relating to power in rowing. A response to my Newsletter from 2018/09 can be found here:
Please see the discussion so far in it's entirety - (text in black after < mark is the citation from the response of our respected opponents, text in blue after VK: mark – is my text).
<1. Application of Newton's Laws starts with choosing the "free body", i.e. the system to be analysed; here the free body is the "rower". Newton's Second Law states that the sum of all forces on any system determines mass of the system multiplied by the acceleration of the system's centre of mass, relative to an inertial frame of reference; for the applications at hand, any frame of reference attached to the Earth's surface or moving with a constant velocity relative to the Earth's surface can be considered inertial; see in-depth analysis below for the consequences of using a non-inertial frame of reference.
VK: Firstly, definitions of power and “Application of Newton's Laws” (analysis of how power is transferred into motion and kinetic energy ) are two different areas and utilise different analysis methods.The first area targets how the power is PRODUCED, the second one – how it is USED.
E.g.: in a car, the definition of power production in the engine is very simple: this is a product of torque on the crankshaft, and it's rpm. Engine power does not depend on accelerations and movements of the car and could be determined accurately and reliably, if two of it's components are measured. Similarly, in rowing and cycling, there is only one channel of power transfer to the external environment: the oar in rowing and the crankshaft-chain in cycling. Other sports are not as simple, so have to use more sophisticated methods, which the Van Ingen Schenau article tried to review.
In the abstract of article (1) of our respected opponents, it was written: “In rowing, instantaneous power output is commonly determined as the dot product of handle force moment and oar angular velocity. The aim of this study was to show that this commonly used proxy is theoretically flawed and to provide an indication of the magnitude of the error.” There is nothing “theoretically flawed” and no error in this fairly simple, yet effective method of power calculation, as well as in the similar method in cycling (crankshaft torque x rpm). The issue here, is that power production and power usage areas were mismatched, which made things quite complicated.
Secondly, if one wishes to analyse the area of power conversion into motion and kinetic energy, I would say that “Application of Newton's Laws” starts with choosing the reference frame first, the “free body” second, followed by it's interaction with the environment. In the 2018/09 Newsletter, three reference frames and three definitions of rowing power were defined: rower, oar and environment (water surrounding the boat). It looks like our respected opponents chose to use the third (but mismatched water with land – a boat goes in the water, not on the land), but my point, is that the “free body” can only be the whole rower-boat-oar system, not the rower on their own. A clear reason for this is the following: rowers (and cyclists) do not transfer power to the environment directly as swimmers and runners do. In rowing and cycling there is a gear mechanism, which converts the power: decreasing force, but increasing velocity. Only blade and drag forces are external relative to the rowing system, all other forces applied by the rower (handle, stretcher forces, etc.) are internal ones (caused by interaction of the athlete with mobile equipment) and cannot be referred to the environment directly. Therefore, it is not possible to analyse only the rower’s kinetics using the environment reference frame, ignoring the boat-oar gearing mechanism. This was the primary reason for any mistakes made.
<2. For any passive mechanical system (e.g. a rigid body), the instantaneous power equation (again using an inertial frame of reference) can be derived from Newton's Second Law. In case no pure moments are applied to this rigid body, the instantaneous power equation simply states that the sum of the power of the forces equals the time derivative of the total kinetic energy. Here, the power of each force acting on the rigid body is defined as the dot product of the force vector and the velocity vector (relative to the inertial frame of reference used!) of the point of application of this force.The outcome of this dot product is identical to the outcome of Kleshnev's equation 1 in the Rowing Biomechanics Newsletter.
VK: Again, to determine the power PRODUCTION directly by means of measuring force x velocity or torque x rpm products between the power source and recipient, the reference frame does not have to be inertial, which I tried to explain with an example of a weightlifter on a rocket, an example that hasn't been answered to.
If we analyse power transformation into kinetic energy, then yes, acceleration of a non-inertial reference frame would add some extra kinetic energy, which was supplied not by the subject (rower), but from external sources. What our respected opponents are missing here is velocity, and the reason for this is that they did not clearly define where the power/kinetic energy is coming from. I hope the following example would help to understand this better.
Imagine a person running on a train, accelerating and having to push the train floor backwards with a force Fah, which creates an equal and oppositely directed reaction force Frh.
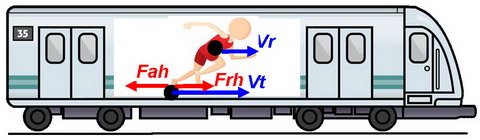
- If the train is stationary, then this is an inertial system and power produced by the runner Pr equal to the gain of its kinetic energy dEk:
Pr = Frh * Vr = 0.5m (Vr22 - Vr12) = dEk (1)
where Frh is a horizontal component of the ground reaction force, Vr, Vr12, Vr22 , - average, final and initial velocities of the runner's CM, m - mass of the runner.
- If the train is accelerating, but the person is standing still, then they still has to apply some ground force to overcome inertia, but they produce zero power because the velocity of his CM is zero relative to the train. In definitions of our respected opponents the person would produce power, because they are moving relative to the “world”. In fact, all power and gain of kinetic energy is supplied by the train engine:
Pr = Frh * Vt = 0.5m (Vt22 - Vt12) = dEk (2)
Where Vt is the train velocity relative to a stationary observer.
- If both the train and runner accelerating, then they produce their own power and contribute their own shares (dEk.train and dEk.runner) into the gain of kinetic energy of the runner:
Ptrain = Frh * Vt = 0.5m (Vt22 - Vt12) = dEk.train (3)
Prunner = Frh * Vr = 0.5m (Vr22 - Vr12) = dEk.runner (4)
Note, that if we measure Frh and Vr directly,we still determine the runner’s power correctly, even though this is non-inertial reference frame. However, velocity Vr must be relative to the train,not to the ground.
- Finally, when the train reaches a constant velocity, it becomes an inertial system, and according to Galileo's Relativity Principle, all mechanics should obey the same laws as in the stationary train. If a runner is accelerating in these conditions, they would produce the same power as in the stationary train, and the gain of their kinetic energy relative to the train would be the same as in the equation 1 above. The train adds no power to the runner and does not increase his kinetic energy, because it moves with constant velocity. However, if we define the runner’s power and gain of kinetic energy relative to the “world”, it will be huge, because Vt >> Vr. Where is this extra energy coming from? This is the energy, which the train accumulated during it's acceleration, and it has nothing to do with the runner’s power and energy. If we would define the runner’s power and gain of kinetic energy relative to the “world”, they would run on the ground and overtake the train.
In rowing, the rower’s power is the only source of mechanical energy, so it is USED to accelerate both the “train” (boat) and the rower's own mass. However, in continuous rowing, which we are discussing, the minimal velocity, and so the kinetic energy at the start of the stroke cycle is not zero – the boat and rower are moving with some speed. Therefore,the gain in kinetic energy during the drive is not relative to the stationary “world”, but relative to some speed-energy, which was accumulated before, during the acceleration at the start.
<3. For an active mechanical system (e.g. a rower), all that has to be added to the passive-system power equation is a term on the left-hand side representing the net mechanical power generated/dissipated within the active system; in the case of the rower, it makes sense to label this term Prower, representing the net mechanical power generated by the rower.
VK: This is either a completely incorrect model, or I have completely missing the point. The rower’s power Prower is the same power which is applied at the handle and the stretcher and is used to accelerate the whole rower-boat system. Adding this would double the power in the system. There is no other power source in the system, except the rower. I specifically asked our respected opponents if there is a misspelling in your Eq.4 below
Prower+ Fxfeet∙vxfeet + Fxhands∙vxhands = mrower∙axrower∙vxrower (eq.4)
And it should be written as
Prower= Fxfeet∙vxfeet+ Fxhands∙vxhands= mrower∙axrower∙vxrower (eq. 4)
However, they insisted on it, but haven’t explained how this power Prower is defined.
My apologies, but I simply do not understand this logic.
4. When all the terms in the power equation for an active mechanical system are averaged over a full cycle of periodic motion, the term describing the time derivative of the total kinetic energy vanishes. This is because the total kinetic energy at the start of a periodic motion cycle i+1 is then identical to that at the start of periodic motion cycle i; consequently, the average change in kinetic energy per unit time is zero during periodic motion.
VK: Yes, “the average change in kinetic energy per unit stroke cycle time is zero during periodic motion”, but this is only because the kinetic energy accumulates due to rowing power in the drive and is used in the recovery to overcome drag. The drive and the recovery are very different phases in the essence of their mechanics, so we have to analyse them separately, if we want to study the conversion of rowing power into kinetic energy. Zero gain in kinetic energy over the stroke cycle only means that it's gain during the drive is equal to it's expenditure during the recovery.
<Points 1-4 above are all that is required to define the average power equation for the active "rower" system during steady state periodic motion, relative to an inertial frame of reference. When we focus on the two forces acting on the rower that have a high associated power (force of oar on hands, force of stretcher on feet), equation 2 in Kleshnev's newsletter (taken from Lintmeijer et al., 2018) is obtained. Thus, this equation follows directly from the basic theory of classical mechanics, and there is nothing incorrect about it.
In his newsletter, Kleshnev has unfortunately failed to notice that (in line with the theory summarised in 1-4 above), Fo,r and Ff,r in equation 2 are forces acting from the oar and from the stretcher on the rower, and not the other way around, as Dr. Kleshnev suggests ("… where For/Ffr are the forces which the ... rower applies to the ...oar handle / stretcher"). Perhaps this misreading of our paper lies at the heart of his misinterpretation of our claims.
VK: This doesn’t change anything in principle, because the reaction force is equally and oppositely directed to the action force (the 3rd Newton law). Yes, the force acting on a rower is a sum of the handle and stretcher forces, but your Eq.2 is completely incorrect in terms of velocities: a rower does not interact with the “world” directly, but with the rowing system, which moves with some velocity relative to the “world”. I hope the previous example with the train and runner will help to understand this.
Also,the Eq.2 is incorrect in terms of the direction of forces: the stretcher reaction force is positive, but the handle reaction force is negative (opposite to the boat's velocity), which means a huge negative power is applied to the handle during the drive (force and velocity are oppositely directed), which is untrue when discussing “power generated by the rower”
<In any case, his conclusion that the average mechanical power generated by a rower is correctly captured by systems considering pin force and oar rotation only, is incorrect. Fortunately, as shown in Lintmeijer et al. (2018),the measurements of pin force and oar rotation can still result in a useful estimate of the true value of Prower if a simple correction is made.
VK: I did not say this. In Newsletter 2018/09, I said: “The power created between the pin and the oar handle can be called the “Net power”, which is transferred through the oar shaft to the spoon, so this is the only source of energy which moves the rower-boat system forward”. I called “Mechanical power generated by a rower” - “Gross power” “which is applied to both the handle and the stretcher in the ratio of about 60%/40%. Gross power is higher than Net power by 4-7% due to inertial energy losses spent on the relative movements of the rower and boat”. And finally: “the Net power transferred from a rower to the external environment is the most important (and the most practical) indicator for the evaluation of a rower’s performance.”
I don’t think it is make sense to discuss any further mathematics in detail, because the base model is incorrect. I can only mention the following passage of our respected opponents, which proves their own mistake:
<Effect of the velocity of the (inertial) frame of reference on Prower
Now it can be readily appreciated that most of the terms in the equation above depend on the choice of frame of reference. In fact, all terms; except Prower! Here’s the proof:
Say we change the velocity of the frame of reference by the velocity “vxextra” (vxextra could be the extra velocity because of a tail wind or caused by rowing in a larger boat). We now have:
Prower+ Fxfeet∙(vxfeet+vxextra) +Fhands∙(vxhands+vxextra) = mrower∙axrower∙(vxrower+vxextra) (eq. 5)
Factoring out parts of the equation yields
Prower+ Fxfeet∙(vxfeet) + Fxhands∙(vxhands) + (Fxfeet+Fxhands) ∙vxextra = mrower∙axrower∙(vxrower) +mrower∙axrower∙vxextra (eq. 6)
If you look closely at the equation above, you see that from equation 3 it follows that the terms (Fxfeet+Fxhands)∙vxextra and mrower∙axrower∙vxextra cancel each other out. What is left is the original power equation, equation 4.
Conclusion: Prower is independent of the choice of frame of reference, but the other terms are not. For rowing, it does not make much sense to discuss handle power and foot-stretcher power separately.
VK: Yes, above is true for the definition of power PRODUCTION P=F v, so you just confirmed my example above about the crankshaft in a car. However, here our respected opponents try to analyse power USAGE into kinetic energy, where “power is equal to the gain of kinetic energy”
The choice of the reference frame does affect the gain of kinetic energy:
0.5 m (V22 – V12) ≠ 0.5 m ((V2+ Vextra)2 – (V1 + Vextra)2)
The right side of this equation is larger, and the difference is exactly what I tried to explain above: this is kinetic energy of the “train”, or in rowing, the kinetic energy of the system accumulated before the stroke cycle in continuous rowing.
The choice of the reference frame is absolutely important and must be unique, if we want to get correct numbers in analysis of power transformation into kinetic energy.