Advanced Analysis of Blade Work

In a previous Newsletter, we found that the blade normal velocity in the water became negative (i.e. the blade centre is moving toward its rear surface) just after the catch and just before the finish. This all happens while the blade is producing some propulsive force, so blade efficiency was calculated higher than 100% at these phases. Here we try to explain this paradox.

The most obvious hypothesis is an effect of oar bend, which was not yet included in calculations of the blade velocity. To evaluate this effect, we calibrated the stiffness of oar shaft by applying dynamic force at the middle of a blade and measuring its displacement. The shaft stiffness was extremely linear (r=0.99) within the range of 0.68-0.91 mm/N for sculling oars (the higher – the softer shaft), and 0.59-0.73 mm/N for sweep oars. These numbers are slightly higher than oar manufacturer’s data because they measure displacement at the end of the shaft rather than at the centre of the blade as we did.

Fig.1 shows curves of the force (a) and blade work (b) (port-side oar of M1x at 34.5 spm) in conjunction with normal blade velocity in the water (c): Vbn calculated as before (RBN 2018/05), Vbb - produced by the oar bend, Vbn+b - corrected blade velocity, which is the sum of two above. Fig.1d shows two blade efficiency curves: Ebl calculated as before (RBN 2007/12), and Ebl+b - corrected for the oar bend.

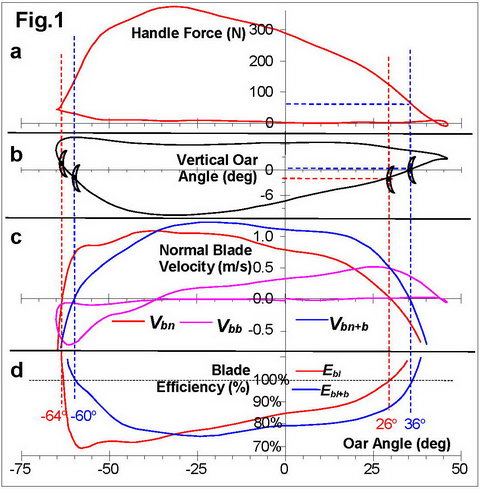
The effect of the oar bend was very significant: it creates blade velocity comparable with its movement in the water, so oar bend must be included into calculations of blade efficiency. The corrected blade velocity Vbn+b became negative at -60o catch, and at 36o finish angles (4o and 10o later than Vbn). The corrected blade efficiency Ebl+b crossed the 100% level at the same oar angles and its curve became more symmetrical, while the average value remained similar (82.1% and 82.0%).

However, oar bend does not fully explain the paradox because a positive force was still measured while the blade centre moved in a rearward direction during 5o after catch and 4o before zero force at finish. Thus, blade efficiency was still higher than 100% during these phases.

Fig.2 illustrates a further idea that can help to resolve the paradox: blade rotation in the water makes velocity of its outer edge faster, so it still moves in the blade frontal direction, while the blade centre and its inner side move to the rear of the blade. Because the blade centre is located approximately at the water surface level at above critical points (Fig.1b), the inner edge is already out of water, so its rear movement does not produce any force. The outer edge is still submerged into under the water, so its frontal movement produces a propulsive force.

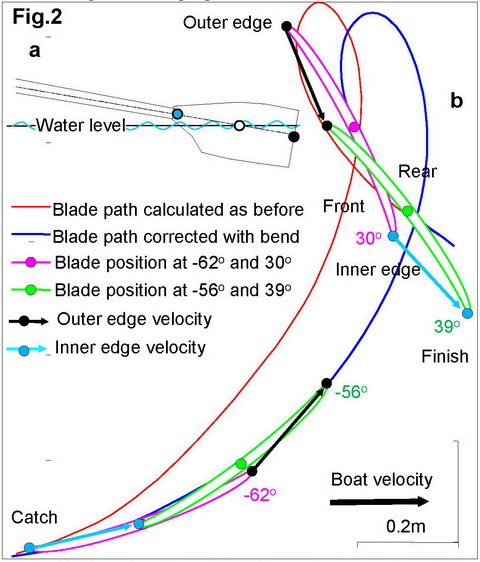
Fig.3 shows velocities of the inner and outer edges of the blade, and its centre corrected with oar bend (a), and corresponding efficiencies (b). The critical points for outer edge fit perfectly to the force curve: at 40o finish angle the measured force decreases down to zero, and small force at -64o catch angle is an effect of oar inertia (RBN 2018/03).

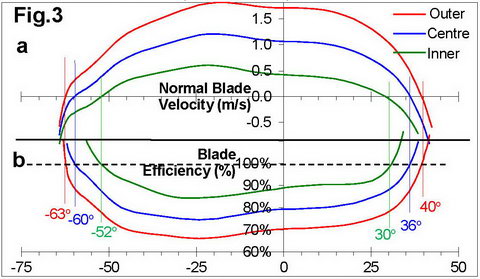
In conclusion, advanced analysis of the blade work allowed reasonable explanation of the blade efficiency calculations, where its values above 100% at catch and finish mean rear movement of the blade centre above water level, without contribution to propulsive force.

©2018 Dr. Valery Kleshnev www.biorow.com