Axial force at the blade

The finer points of oar mechanics were previously analysed in RBN 2020/12: discrepancies between propulsive forces derived at the blade and rower-boat system were found, and a hypothesis was raised about the possible contribution of the blade axial force. Since then, we have tried different ways of measuring the blade axial force directly with a sensor built in the shaft close to the blade. However, attempts were unsatisfactory because of high crosstalk from a large torque created by normal blade force. So, it was decided that axial blade force F_ba would be determined indirectly, as a difference between the handle F_ha and gate F_ga axial forces:

F_ba = F_ha – F_ga                                           (1)

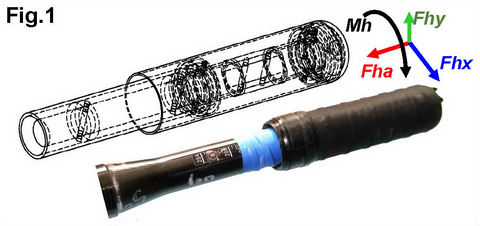
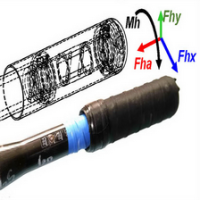
To do this, a new type of force sensor was developed by BioRow (Fig.1), which was inbuilt into a handle of a sculling oar and can measure 4D forces:

1. Axial handle force F_ha;
2. Horizontal (at squared blade) handle force F_hx;
3. Vertical (at squared blade) handle force F_hy;
4. Twisting torque at the handle M_h.

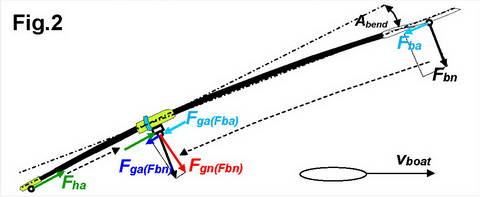
After the sensor was tested and the data analysed, it was found that the equation is not as simple as above (1). The reason was the bend of the oar shaft A_bend (Fig.2), which makes the blade angle different from the gate angle relative to the boat. This means that the normal blade force F_bn transferred through the shaft is not orthogonal to the gate axis, so it can be decomposed into two components: normal F_gn(F_bn) and axial F_ga(F_bn), which must be taken into the equation:

F_ga(F_bn) = F_bn sin(A_bend)                           (2)

The real axial force at the blade F_ba created by water flow also transferred through the shaft to the gate as F_ga(Fba) and also becomes slightly angled to the gate axis:

F_ga(Fba) = F_ba cos(A_bend)                             (3)

The final equation used to derive the axial blade force F_ba from the measured gate F_ga and handle F_ha axial forces was the following:

F_ba = (F_ha –(F_ga + F_bn*sin(A_bend)))/cos(A_bend)     (4)

The normal blade force F_bn in this equation was derived from torques measured at the shaft (see RBN 2020/10), and the bend angle A_bend - from the blade force F_bn using a shaft stiffness factor for each oar.

The data was collected in M1x (1.85m, 88kg) performed six pieces 15-20 strokes each with step-increasing stroke rate from 20 to 40spm. Fig.3 shows derived axial forces on the port-side Smoothie blade at the stroke rate 35.5spm:

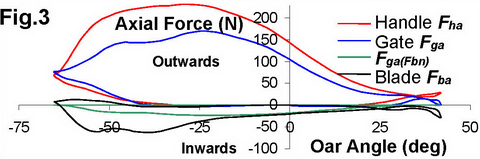
As expected, the axial force measured at the handle F_ha was significantly higher than at the gate F_ga, a small part of the difference (max. 25N) can be explained by transferred axial component of the normal blade force F_ga(Fbn), and the main part (max. 75N) should be related to a real axial blade force F_ba.

Fig. 4 shows the real axial blade force F_ba of the port-side Smoothie blade at various stroke rates, plotted together with corresponding blade work profiles:

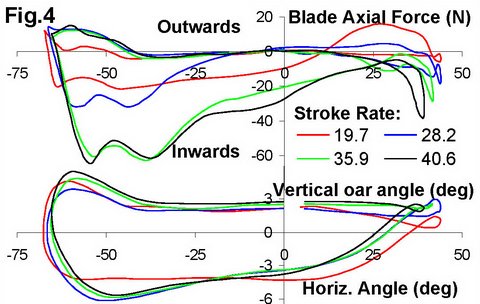
During the first part of the drive, the axial blade force F_ba was always directed inwards (from the blade to pin), and its magnitude increases with the stroke rate from about 20N up to 60N, which can be well explained by increased drag resistance at higher speed. After perpendicular oar position, the axial blade force F_ba is directed outwards at low rates, which also can be explained by the drag, but at higher rates it was still directed inwards till the finish, though at smaller magnitude, less than 20N. This fact needs further interpretation, we can only guess that it could be related to the blade work profile: with increasing of the stroke rate, it is getting deeper after catch, but shallower before finish.

Concluding, the axial blade force was found to be quite significant: it can create up to a 70N braking force with two blades at oar angles 55deg, which is similar to the drag at the boat hull. Therefore, blade resistance at its axial movement through the water should be minimised.

Acknowledgements: Thanks to Concept2 Inc. and personally to Dick Dreissigacker and Alex Dunne for the interest and kind support of this study.

©2021 Dr. Valery Kleshnev www.biorow.com