Refined balance of propulsive forces

The determination of the fine balance of propulsive forces in the rower-boat-oar system is important for understanding the exact mechanics of force and power transmission from the blade hydrodynamic forces – to the movement of the system. Clear understanding of these mechanics would help to optimise efficiency of the system and improve performance. Previously, it was not possible to obtain this balance accurately and discrepancies were found between the blade propulsive force (defined in that way) and the force acting on the rower-boat system (RBN 2019/02, 2020/12). With our latest BioRow developments: the method of determination of the exact centre of pressure (CP) on the blade (RBN 2020/10) and 4D instrumented handle (RBN 2021/06) measuring the axial handle force, it became possible to complete the puzzle and derive the exact balance of propulsive forces in rowing.

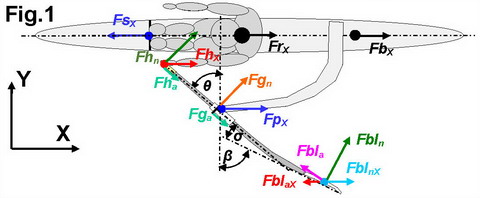
The measurements were made in the same instrumented single as before (RBN 2019/01-2), so we won’t repeat the description. The propulsive force Fb_X at the boat (Fig.1) was also defined as before, as the difference between the pin Fp_X and stretcher Fs_X forces (sum of opposite vectors):

Fb_X = Fp_X – Fs_X                                        (1)

The propulsive force applied to the rower’s centre of mass CM Fr_X was defined as the difference between the stretcher reaction force Fs_x and the resultant X handle force Fh_X, where the latter is the vector sum of X components of normal Fh_n and axial Fh_a handle forces. Previously (RBN 2019/02), it was assumed that Fh_a is equal to the measured axial gate force Fg_a, and “they could be slightly different”, which appeared to be not quite true. Now, the axial handle force Fh_a was measured directly with our new BioRow 4D instrumented handle (RBN 2021/06) and used in the equation for the rower’s propulsive force Fr_X:

Fr_X = Fs_X – Fh_X = Fs_X – (Fh_n cos(θ) + Fh_a sin(θ))   (2)

The system propulsive force Fsys_X was defined as the vector sum of the boat and rower’s CM forces:

Fsys_X = Fr_X + Fb_X                                     (3)

The normal blade force Fbl_n was defined in RBN 2020/10 from the measured torque at the oar and actual outboard calculated using CP position at the blade. The axial blade force Fbl_a was derived as in RBN 2021/06: as the vector sum of axial forces at the handle Fh_a and gate Fg_a, with correction for transfer of the normal blade force caused by oar bend angle σ:

Fbl_a = (Fh_a – Fg_a - Fbl_n*sin(σ)) / cos(σ)  (4)

The total blade propulsive force Fbl_X was defined as the vector sum of X components of the blade normal Fbl_nX and axial Fbl_aX forces:

Fbl_X = Fbl_nX + Fbl_aX = Fbl_n cos(β) + Fbl_a sin(β)   (5)

where the blade angle β was calculated as the sum of measured oar angle θ and shaft bend angle σ derived from oar stiffness factor and blade normal force Fbl_n:

β = θ + σ                                                      (6)

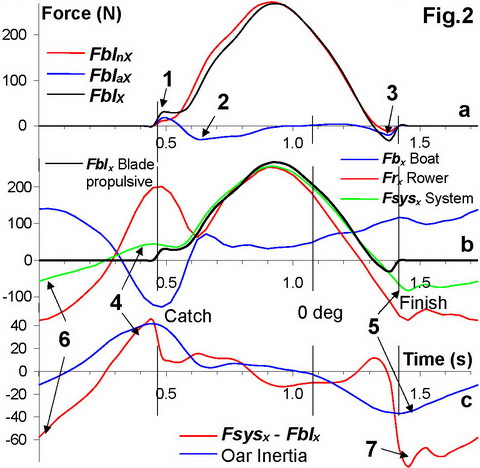
At the very beginning of the drive (Fig.2,a, data in M1x at 34spm), the blade axial force is the main contributor to the oar propulsion (1), but then it plays a negative role and creates a braking force during the first half of the drive (2) and before the finish (3). Therefore, it is important to minimise the drag caused by axial blade force and make the blade and boat surface as smooth as possible.

The curves of propulsive forces at the blade Fbl_X and the rower-boat system Fsys_X were very similar (Fig.2,b) and correspond much better than in previous experiments, so their average values over the drive differ only by 0.5%. The main reason of the difference between the curves was the inertial forces of the blade (Fig.2,c), which increase to the system propulsion Fsys_X at the catch (4, oar rotation decelerates and inertia pushes pins forward), but decrease it after the finish (5, oars accelerate and pushes pins backwards). The cause of excessive braking force during the middle of recovery (6) could be the aerodynamic drag of the oars. After the finish (7) – hitting water with feathered blades (the average Fsys_X - Fbl_X over the cycle was -15N).

Concluding, the main achievement of this study was to obtain the refined balance of propulsive forces in the rower-boat-oar system, which confirms the validity of our models, accuracy of the measurements, and allows further extended studies and optimisation of rowing biomechanics.

Thanks for help with this study to my wife Katerina, Marlow RC coach, who sadly left us on the 8^th September.

©2021 Dr. Valery Kleshnev www.biorow.com