New method of kinetic energy evaluation

The studies of propulsive and
drag forces (RBN 2019/01-02) were done with the hope to analyse the conversion
of rowing power into kinetic energy, which was intensively discussed last year
(RBN 2018/09,11). It is still not possible to verify my model with experimental
data, because of the uncertainty in the calculation of the propulsive force
(RBN 2019/02). Nevertheless, a new method of kinetic energy evaluation was recently
developed, which may help to solve the propulsive force puzzle, and also could
be valuable on its own, because it is quite simple and requires only the boat
velocity, oar angle and seat position data.
The method is based on the assumption that, at the catch and finish, when the oar and rower’s mass are changing direction, the velocity of the rower’s CM relative to the boat is close to zero, so absolute velocities of the rower’s mass and the boat are nearly equal. This means the velocity of the whole rower-boat system CM could be easily determined with instantaneous boat velocity at the catch and finish. During all other phases of the stroke cycle, movements of the rower’s body segments are quite complex, and more sophisticated methods are required to determine the velocity of the system’s CM.
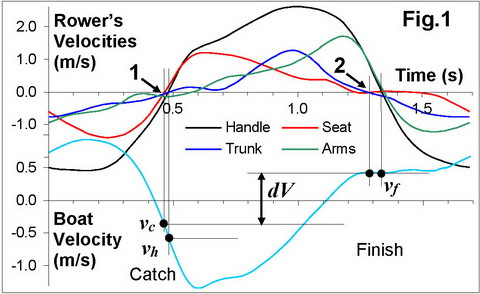
At the catch, the rower’s CM is
closer related to the seat movement, than to the handle, which is connected to
relatively lighter masses of arms and upper body. Therefore, the moment when
the seat velocity crosses zero upwards (Fig.1,1) was chosen as the primary
trigger to take the starting boat-system velocity vc. If the
handle movement would be taken as the trigger, the boat velocity value (vh)
would be quite different, as it changes rapidly at the catch.
At the finish, though it would
be logical to associate the rower’s mass with the trunk velocity (Fig.1,2)
rather than with the handle, it doesn’t make a significant difference, because
the boat velocity is nearly constant. So, the moment when the handle velocity
crosses zero downwards was taken as the trigger to take the final boat-system
velocity vf.
During the drive, the gain in kinetic
energy of the rower-boat system dEk is the difference
between its final and starting values:
dEk = M vf2/2
– Mvc2/2 = 0.5M(vf2-vc2) (1)
where M is the full mass of the
system equal to the sum of the boat, rowers and oars masses. Table 1 shows
values of kinetic energy calculated with this method in M1x (1.84m, 84kg) at
various stroke rates.
Work per stroke WpS
was determined directly with the standard BioRow
measurements. The values of dEk calculated with the
new method were lower than the measured WpS, and their average ratio was
52.7%, which could be explained as follows:
·
During the drive, 23.7% of the energy produced by the rower was lost in
the blade slippage (average blade efficiency Ebl was 76.3%).
· 23.6% of WpS (on average) was spent on overcoming the drag resistance in water and air.
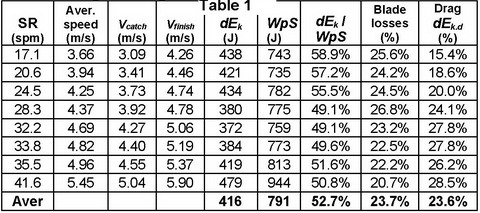
The percentage of the drag expenditures
increases nearly twice with the increase of stroke rate, which is explained by
changes in the rhythm: at 17 spm, the drive time consists only 35.1% of the
cycle time, but at 41 spm it was 53.6%. This was confirmed by a very high
correlation of drag energy shares with the rhythm (r=0.984).
During the recovery, there is
no propulsive power produced by the rowers, so the kinetic energy of the system
decreases from its maximum at the finish to the minimum at the catch, being
used to overcome the drag forces. Therefore, the reversed values of dEk
could be used for the evaluation of the energy spent on overcoming the external
drag. It was found that at the racing stroke rate 35.5spm, about
two thirds (66.3%) of the drag energy is spent during the recovery, and only
one third (33.7%) – during the drive, in spite of their durations being nearly
equal (rhythm was 50.8%). This
happened because the boat speed is higher during the recovery (106.2% of the
average) than during the drive (85.7%). At lower rates, the shares of energy
spent during the recovery were even higher, because the recovery time is
relatively longer.
To verify the new method, the gain of kinetic
energy dEk.test was calculated from the measured WpS,
energy losses for the blade slippage Wbl = WpS*(1-Ebl)
and energy spent on the drag over the drive phase Wd (based on the
measured boat velocity and drag factor):
dEk.test = WpS – Wbl - Wd (2)
In the samples above, kinetic energy dEk calculated with the new method had high correlation with dEk.test (r=0.94), and on average, dEk was 14.8% higher. This means that the new method produces quite reasonable values for kinetic energy, even without force measurements. The fact that the new method produces slightly larger values of kinetic energy could be an indirect confirmation of the hypothesis that the real blade propulsive force is higher than one calculated from the handle force (RBN 2019/02), but the reasons for it are still not clear.
©2019 Dr. Valery Kleshnev www.biorow.com



