Balance of forces on the boat hull

Experiments with comprehensive force measurements were conducted recently with new the BioRow instrumented C-bracket, which was mounted on a wing rigger (Fig.1) and measured 3D force at the pin: in horizontal Fp_H, side Fp_S and vertical Fp_V directions. Forces at the gate were measured with the BioRow 2D instrumented oarlock at the normal to the oar axis Fg_N and axial direction Fg_A.

The stretcher force was determined at three points with BioRow v.2009 sensors (RBN 2013/08), which measured the horizontal force components Fs_H only (Fig.2).

Other biomechanical variables were measured with the standard BioRow system (Fig.3): oar angles in horizontal Ah and vertical Av planes (RBN 2009/10), seat and trunk movements (2014/12), boat speed, acceleration and rotations (2012/03), wind speed and direction (2013/06).

A male sculler (1.84m, 84kg) performed 8 short rowing pieces of ~200m each, increasing stroke rate from 17.2 up to 41.5 spm. The data for each sample was processed using the standard BioRow method (RBN 2017/12), and the penultimate sample of 35.5spm is presented below (Fig.3).

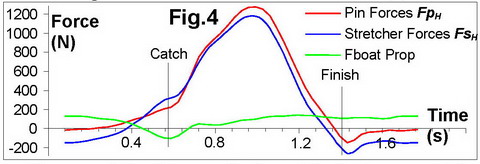
The sum of three stretcher forces Fs_H was subtracted from the sum of horizontal components of both pin forces Fp_H, which resulted in propulsive force applied to the boat hull Fb_H (Fig.4):

Fb_H = Fp_H - Fs_H                                               (1)

The propulsive force at the boat Fb_H is the sum of the boat inertia force m_b a_b (m_b=16.7kg is the full boat mass, a_b is its acceleration) and drag force at the hull F_d, which could be determined directly from our measurements.

F_d = Fb_H - m_b a_b                                               (2)

This drag force calculated with our force measurements F_d(F) was compared with the drag force calculated from the boat velocity v and drag factor DF: F_d(v)=DF v², and the difference was determined as D_Fd= F_d(F)- F_d(v).

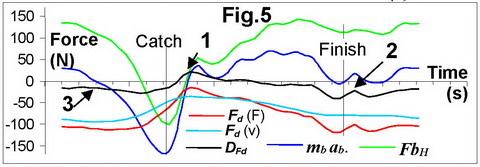
The curves of the drag force calculated with different methods appeared to be quite close (Fig.5). The small difference could be explained by the force on the slides, which arises from two factors: gravitation and friction. After the catch, the boat pitch has maximal negative values of about -1deg (stern – down, bow - up), plus a 1deg slides pitch relative to the boat. The rower’s mass moves slightly upwards, which creates forward force at the slides F_sl=sin(A_p) m_rg. At the total slide angle A_p=2deg and the moving rower’s mass m_r=60kg (weight of legs subtracted), a force F_sl of ~20N pushes the boat forward at slides, but it was not measured and accounted for here in the force balance. Therefore, the drag force F_d(F) was calculated higher than its real value (Fig.5,1).

During the drive, the boat pitch became positive up to +1deg (stern goes up, bow – down), so the slide angle became close to zero and only the friction force at the wheels of the slide affects the total balance of forces. At the finish, this creates a few fluctuating peaks (2), when the seat moves fore-aft and may hit back-stops. During the recovery, the friction force at the seat pushes the boat backwards, which shifts the measured balance of forces in a negative direction (3).

The average drag force Fd over the stroke cycle was compared with the average boat speed v for each of eight samples. It was found that the best fit equation is different from the traditionally used: Fd= 2.59 v^2.1726 (R² = 0.989). In fact, the average F_d(F) was found to be ~12% higher than F_d(v). This will be further discussed in future publications.

Concluding: For the first time, the drag force on the boat was determined directly with BioRow measurements, which can be used for evaluation of rowing technique and equipment quality.

©2019 Dr. Valery Kleshnev www.biorow.com