Power And Kinetic Energy In Rowing
Power and kinetic energy
Recently,
we had an interesting discussion with Mathijs Hofmijster about power in rowing
(full
text is here). The point I made is that power measurements and the ŌĆ£Applications
of Newton's LawsŌĆØ (analysis of the power transformation into motion and kinetic
energy, which Mathijs tried to do) are two different areas and utilise
different methods of analysis. The first area targets how the power is PRODUCED;
the second ŌĆō how it is USED.
For
example: in a car, the definition of the engine power production is very
simple: a product of torque on the crankshaft by its rpm. Engine power does not
depend on accelerations and movements of the car and could be determined
accurately and reliably if two of its components are measured. Similarly, in
rowing and cycling there is only one channel of power transfer to the external
environment: the oar in rowing, and the crankshaft-chain in cycling. Other cyclic
sports (running, swimming, canoeing, skiing, etc.) are not as ŌĆśluckyŌĆÖ- they
require more sophisticated methods to calculate power production. Therefore, net rowing power can be determined
accurately and reliably with force-velocity or torque-rpm measurements at the
oar. No arguments were presented to disprove this statement yet.
Analysis
of a rowerŌĆÖs power conversion into motion and kinetic energy of the rowing
system starts with choosing the reference frame (RF), followed by the ŌĆ£free
bodyŌĆØ, and then its interaction with the environment. If the RF related to the environment
is chosen (water surrounding the boat, not the ŌĆ£EarthŌĆØ, i.e. the shore,
proposed by our respected opponents), the ŌĆ£free bodyŌĆØ can only be the whole
rower-boat-oar system, not the rower themselves. An obvious reason for this is the
following: rowers and cyclists do not interact with the environment directly (as
runners and swimmers do): they transfer power through a gear mechanism, which
converts the power by increasing velocity, but decreasing force. In rowing, only
the blade reaction force and the drag force at the hull are external relative
to the rowing system. All other forces applied by the rower (handle, stretcher,
gate forces) are internal ones and cannot be referred to the environment
directly. Therefore, it doesnŌĆÖt really make sense to multiply internal forces
by their velocities relative to the external environment, which is what our opponents
have done.
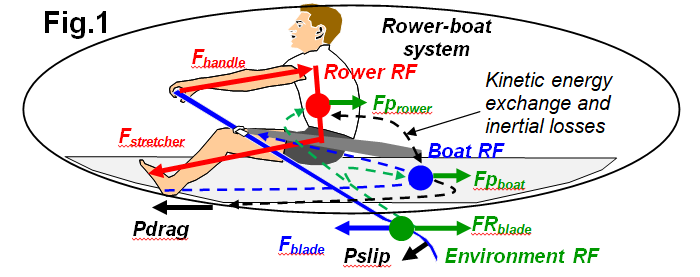
Here
is our model of power transformation into kinetic energy in rowing (Fig.1), excluding any mathematics for simplicity.
1.
The rower is the only source of energy that
moves the whole rower-boat system. The rower applies Gross Power at the handle and the stretcher, which should be
defined using the rowerŌĆÖs CM as the reference frame. This is a non-inertial RF,
but this does not affect power calculations if forces and velocities are
measured directly.
2.
From the rower, power is applied to the oar and
becomes Net Power transferred to the
external environment. As the oar rotates around the pin mounted on the boat, the
boat RF should be used. This is also a non-inertial RF, but again the Net Power
is determined correctly if the oar torque and angular velocity are measured.
3.
In this transformation between RFs, some power
is lost in relative movements between the boat and rower (inertial losses), so
Net Power is lower than Gross Power by 5-7% (RBN 2010/05).
4.
At the oar, the Net Power is converted: the
blade velocity is nearly doubled compared to the handle velocity, and the force
proportionally decreases.
5.
The blade force is applied to the water, which
creates an opposite reaction force, moving the whole system forward. In this
case, an inertial environment RF based on the water surrounding the boat should
be used. Power converted into kinetic energy of the system is the product of
the forward component of the blade reaction force by the velocity of the systemŌĆÖs
CM.
6.
The velocity of the systemŌĆÖs CM is lower than the
blade velocity relative to the boat, so in this way a proportion of the blade
power (15-20%, RBN 2012/06) is wasted into blade slippage in the water.
7.
The blade reaction force is transferred back
through the oar and shared between the two main components of the system: the
rower and the boat. The shares depend on the ratio of the handle/gate/stretcher
forces and vary during the drive: a higher stretcher force (when a rower emphasises
the leg drive) accelerates the rower, but slows down the boat; higher
handle/gate forces (upper body emphasised) accelerates the boat, but negatively
affect the rowerŌĆÖs acceleration.
8.
The power that is applied to the rower and boat
masses and converted into their kinetic energy is a product of their shares in
the blade propulsive force by their velocities relative to the water in the
environment RF.
9.
Two components of the system, the rower and the
boat, not only receive kinetic energy through the oar, but also exchange it
between themselves. During the recovery, the oar supplies no energy, but the
rower pulls the stretcher and transfers his kinetic energy to the boat, which
accelerates. Energy exchange also happens during the drive: after the catch, the
rower actively accelerates his CM using the leg drive, taking kinetic energy
from the boat, which receives negative acceleration. As this exchange is
provided by the rowerŌĆÖs efforts and has nothing to do with the external
environment, it is logical to suppose that the rower RF should be used, or an
inertial RF moving with constant velocity equal to the average of the system
over the cycle. This makes the analysis quite challenging, because the source
of kinetic energy is not always clear. The complexity is multiplied by the
number of rowers in a crew.
10.
Finally, all kinetic energy is lost in the
water and to air drag resistance. The main part is spent on the water drag at
the hull, which is equal to the product of the boat drag factor by the cube of
its velocity in the water, so the highest losses occur at the highest boat
velocity during the recovery.
The
mathematics of this model will be presented in a future Newsletter, confirmed
with measured data.
┬®2018 Dr. Valery Kleshnev www.biorow.com



