Rowing Power
Several
scientific articles about rowing power were recently published by Dutch researchers
(1, 2), which placed doubts upon the standard definitions of this important
indicator of performance. In this newsletter, I will be reviewing this topic,
which I last discussed in RBN 2004/06 (3,4).
Power is a process of energy
transfer. It must always have an object
which produces energy, and a subject
to which the power is applied. The basic equation of mechanical power P
is:
where force F and velocity v must be between the object and the subject, not relative to something else, and α is the angle between the force and velocity vectors. Quite a common mistake in rowing publications is an incorrect model of power transfer, which mismatches forces and velocities and creates erroneous results. This mistake has been made in the starting equation of the articles 1, 2:
where Fo,r / Ff,r are the forces,
which the object (rower) applies to the subjects (oar handle / stretcher), but vh/w
- vb/w
are
velocities of the subjects relative to “something else” –the “world” reference
frame. However, the outside world does not apply the force and power to the
handle and stretcher – the rower does this, moving at some velocity relative t the outside world, so we must refer to the rower’s centre of mass (CM), not to
the “world”. According to the erroneous equation 2, the rower’s power depends on
other external factors: a rower applying the same handle force and velocity,
would have higher power in bigger/faster boats or in a tailwind, and in
small/slower boats or in a headwind the power would be significantly lower (up
to 20-30% difference), which should not be the case. Moreover, the “world” reference
frame was related to the shore, not to the water: in this way, the rower’s
power depends on the speed of the river current, which is completely untrue.
Previously, I have outlined
three main methods of rowing power calculation (3, 4), and now, we’ll discuss them
in more detail. The methods differ by the choice of the reference system:
1. The “traditional” method is
based on the boat frame;
2. “Propulsive-waste” power is related
to the mass of water surrounding the boat (not to the “Earth”);
3. “Rower’s power” bound to the
rower’s CM.
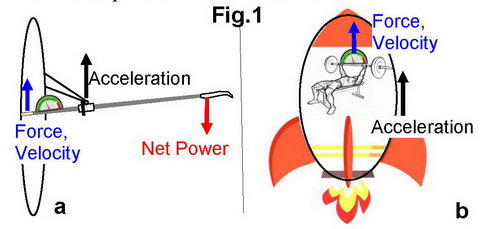
In the “traditional” method, I
noticed that the boat is not an inertial reference frame, because it moves with
acceleration, and this was confirmed in the referred articles. This means, say,
at a 2g boat acceleration, moving a 10kg mass would require 20kg of force,
similar to lifting up a weight inside an accelerating rocket (Fig.1). However,
if the force and velocity are measured directly, the gauge will show 20kg of force,
so the power calculations are correct.
The
power created between the pin and the oar handle can be called the “Net power”,
which is transferred through the oar shaft to the spoon, so this is the only
source of energy which moves the rower-boat system forward. This power is measured
directly and correctly with our BioRowTel
system and the NK EmPower oarlock.
The 2nd power
definition describes the Net power transformation at the blade, where it is
divided between the Propulsive power, which propels the rower-boat system and Waste
power lost in blade slippage. Both components are difficult to measure
directly, so this method is not practical.
The 3rd power
definition is in the rower’s reference frame and could be called “Gross power”,
which is applied to both the handle and the stretcher in the ratio of about
60%/40%. Gross power is higher than Net power by 4-7% of inertial energy losses
spent on the relative movements of the rower and boat (RBN 2010/05). Gross
power is also not very practical to determine: measurement of the horizontal stretcher
force is complicated, and the velocity of the rower’s CM is quite hard to
determine. Also, definition of the Gross power could be extended by the energy
that the rower spends on the vertical movements of the oars, friction on the slides,
etc., so this method is quite uncertain.
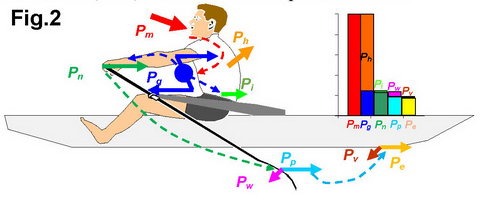
Fig. 2 schematically shows the
process of energy transformation in the rower-boat system. The rower consumes Metabolic
energy Pm and applies mechanical Gross power Pg
to the oar handle and stretcher (24-28% of Pm), while 72-76% of Pm
is heating the rower’s body. About 6% of Pg is spent on inertial
losses Pi and 94% goes to Net power Pn delivered
to the blade, where it is spend on the Propulsive Pp (about 80%)
and Waste Pw (20%) powers. About 6% of Pp is lost due
to variation of the boat velocity (Pv) and the rest is
effective propulsive power Pe.
In conclusion, the Net power transferred from a rower to the external environment is
the most important indicator for the evaluation of a rower’s performance. It is
measured correctly and reliably with BioRowTel and NK EmPower systems.
1. Hofmijster M., Lintmeijer L.,
Beek P., van Soest K. (2018) Mechanical power output in rowing should not be
determined from oar forces and oar motion alone, Journal of Sports Sciences,
36:18, 2147-2153
2. Lintmeijer L., Hofmijster M.,
Fischedick G., Zijlstra P., Van Soest A. (2018) Improved determination of
mechanical power output in rowing: Experimental results, Journal of Sports
Sciences, 36:18, 2138-2146
3. Kleshnev V. (2000) Power in
rowing. Proceedings of XVIII Congress of ISBS, (2) Chinese University of Hong
Kong, 662-666
4. Kleshnev V. (2016) The Biomechanics of Rowing. Crowood Press. 190 p. ISBN 978 1 78500 133 8.
©2018 Dr. Valery Kleshnev www.biorow.com




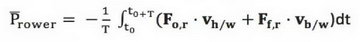 (2)
(2)