Blade Drag Factor
During the drive phase, the blade slips through the water creating a resistive drag force, which is in fact the propulsive force moving the whole rower-boat system forward. The lower the slippage of the blade, the higher its propulsive efficiency. However, the latter depends on the boat’s velocity (RBN 2012/06), which varies depending on boat types, weather conditions and during the stroke cycle and makes its evaluation difficult. So, we proposed to evaluate blade work using a method similar to boat shell Drag Factor DF:
DF = Fdr / v2 (1)
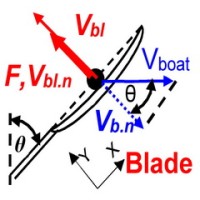
where Fdr is the resistive drag force and v is the velocity of an object moving through a liquid. In the case of a boat shell, it is simple to determine DF, because the boat velocity is linear and the drag force works in the same line. However, the blade trajectory is curvilinear (RBN 2007/12), so it is not quite clear which force and velocity should be used in equation 1. At least three options available here, which use various reference systems (Fig.1):
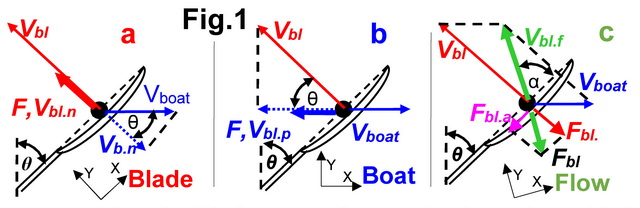
A. Using the blade as a reference (and rotating with it through the drive), the Blade Drag Factor Normal BDFn is defined using blade velocity Vbl.n relative to the water in the perpendicular direction to the blade axis:
Vbl.n = Vbl – Vboat * cos θ (2)
where Vbl is the normal blade velocity relative to the boat (derived from measured angular velocity and actual outboard), Vboat is the measured boat velocity, θ is the measured oar angle.
BDFn = Fbl / Vbl.n2 (3)
where Fbl is the normal blade force (derived from the measured handle force and actual gearing ratio).
B. Using the boat as a reference, the Blade Drag Factor propulsive BDFp is defined using the blade’s velocity Vbl.p relative to the water in the direction parallel to the boat axis – in the propulsive direction, so:
Vbl.p = Vbl * cos θ – Vboat (4)
BDFp = Fbl cos θ / Vbl.p2 (5)
C. If we consider the blade as an object moving through the water, then Blade Drag Factor relative to the flow BDFf is defined by the magnitude of the vectors of the water velocity relative to the blade Vbl.f and the drag force Fbl.f in the direction opposite to the velocity vector. In this case, the reference system is related to the vector of the water flow at each moment of time, of which magnitude Vbl.f could be derived as:
Vbl.f = (Vbl2+Vboat2-2*Vbl*Vboat*cos(θ))0.5 (6)
The direction of the flow vector is defined by the oar angle θ and the blade angle of attack α, which could be calculated as:
α = asin((Vbl.f2 + Vbl2 - Vboat2) / (2 Vbl.f Vbl)) (7)
The magnitude of the drag force Fbl.f in the flow direction is the vector sum of the blade’s normal Fbl and axial Fbl.a forces, but the latter is usually not measured. Hofmijster et al. (1) has found the peak axial blade force Fbl.a in the range 10-13 N, which is only 6-8% of the normal blade force Fbl, so the force Fbl.f and BDFf could be calculated from Fbl only, without significant error:
BDFf =Fbl.f / Vbl.f2 = (Fbl * sin α) / Vbl.f2 (8)
Fig.2,a shows all three drag factors above in M1x at 34.5spm (the sum of two blades) together with corresponding blade velocities (b). As it should be, all three BDFs are nearly equal at the 0 deg. oar angle at about 350, when the normal blade velocity is 100% propulsive (directed parallel to the boat) and water flow velocity is normal to the blade, so is equal to the blade velocity.
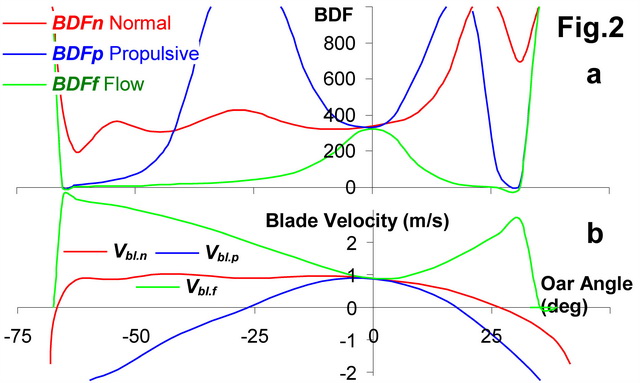
At other oar angles, BDFs behave very differently:
• BDFn is the most consistent from the catch to the 0 deg. oar angle, then it increases to infinity at about the 25 deg. oar angle, when blade velocity Vbl.n crosses zero. After this point it decreases down to zero, while blade force decreases and blade velocity increases, but in the opposite direction: forward with the boat, towards the bow.
• BDFp goes to infinity twice during the drive, at -25 and 20 deg., when Vbl.p crosses zero from negative (towards bow) to positive (towards stern) and back to negative. After the catch and before the finish it is close to zero because the blade force is low, but the blade centre moves fast with the boat.
• BDFf is low at the beginning and the end of the drive, because the velocity of the water flow is high at sharp angles of attack, but the force in this direction is low. It never goes to infinity and its curve has a smooth bell shape.
It is interesting to compare the blade DF with the boat DF, which was 2.95 in this case. So, the blade DF was about 120 times higher than boat DF, and this is is the only reason why the rower-boat system is able to move through the water.
References
1. Hofmijster M., Koning J., Van Soest A. 2010 Estimation of the energy loss at the blades in rowing: Common assumptions revisited. Journal of Sports Sciences, p. 28(10): 1093–1102



